Menilai Eksposur Faktor Suatu Portfolio

Tulisan ini adalah penjelasan awal akan pendekatan untuk menilai eksposur faktor suatu portfolio. Saya berencana untuk memberi link kepada artikel internet yang kredibel untuk penjelasan topik ini, tetapi saya merasa penjelasan akan lebih lengkap dan lebih mendasar (mudah dipahami) jika saya yang menulis penjelasan topik secara langsung. Maka, oleh karena itu saya hendak menulis tulisan ini untuk memberi edukasi dasar kepada investor-investor yang tertarik akan pendekatan faktor, atau hanya ingin memiliki pemahaman lebih terkait pendekatan kuantitatif di pasar modal yang mencakupi model regresi linear dan analisis atribusi performa.

Seperti tulisan “Faktor Momentum” saya sebelumnya, tulisan ini hendak juga dibagi menjadi 12 bagian: 1. Apa itu eksposur faktor, 2. Rumus dasar perhitungan eksposur faktor, 3. Pendefinisian dan konstruksi faktor, 4. Regresi linear sebagai instrumen pengukur eksposur faktor, 5. Sekumpulan asumsi di belakang regresi linear, 6. Interpretasi output penting dari hasil regresi linear, 7. Sekumpulan kesalahan dalam menilai eksposur faktor portfolio, 8. Penentuan “alpha” melalui output “intercept”, 9. Contoh nyata penilaian eksposur faktor portfolio, 10. Peringatan singkat tentang regresi linear, 11. Poin kesimpulan, dan 12. Catatan lainnya. Seperti biasa - referensi, ilustrasi relevan, dan sumber daya lainnya akan diberikan di akhir dari tulisan. Mohon juga diberi tahu di komentar jika terdapat kesalahan atau misinterpretasi dari tulisan yang saya buat, masukan yang relevan hendak diterima selama koreksi telah diverifikasi melalui sumber terpercaya.

1. Apa itu eksposur faktor

Eksposur faktor adalah konsep yang berhubungan erat dengan faktor-faktor risiko sistematis yang berfungsi sebagai pendorong dari performa suatu portfolio aset. Dengan sendirinya, eksposur faktor berfungsi untuk menilai “sensitivitas” suatu portfolio dengan hubungannya terkait dengan premia bagi faktor tertentu, sensitivitas tersebut dapat memiliki pengaruh yang signifikan bagi pengembalian dari portfolio. Sebagai contoh, asumsikan terdapat 1 portfolio; portfolio A; dan terdapat 3 faktor yang mencakupi faktor “a”, “b”, dan “c”; faktor “a” memiliki premia tahunan sebesar 8%, faktor “b” memiliki premia tahunan sebesar 5%, dan faktor “c” memiliki premia tahunan sebesar 2%; untuk portfolio A, portfolio memiliki nilai eksposur faktor “a” sebesar 0.79, nilai eksposur faktor “b” sebesar -0.2, dan nilai eksposur faktor “c” sebesar 1.1; maka, portfolio A diekspektasikan untuk memberi pengembalian sebagai berikut: (8%*0.79) + (5%*-0.2) + (2%*1.1) = 7.52%. Perhatikan bagaimana nilai eksposur portfolio memiliki pengaruh terhadap jumlah premia yang benar-benar terealisasi di dalam portfolio sendirinya, hanya karena suatu portfolio menargetkan faktor “a”, belum tentu portfolio tersebut dapat secara penuh merealisasikan premia 8% bagi faktor “a” sendirinya - perhitungan eksposur masih dibutuhkan untuk memastikan bahwa premia ekspektasian faktor hendaknya cukup signifikan untuk memberi keuntungan di atas pasar (alpha), serta dengan cukup untuk menutupi biaya transaksi dari implementasi portfolio faktor sendirinya.

Studi ekonometrik adalah bidang studi yang berfungsi untuk mengikat teori ekonomi dengan bukti empiris, dan menarik kesimpulan umum (inference, generalization) berdasarkan hasil output dari analisis kuantitatif yang telah dilakukan - output kuantitatif tersebut digunakan untuk memvalidasi teori yang sebelumnya bersifat kualitatif, dan melihat jika teori kualitatif tersebut berdiri di hadapan uji empiris. Praktik penilaian eksposur faktor suatu portfolio pun tidak lepas dari pendekatan ekonometrik sendirinya, dengan penilaian eksposur faktor portfolio yang umum dilakukan dengan alat/model regresi linear - model umum yang dipakai di studi ekonometrik. Fungsi uji sensitivitas bagi analisis eksposur faktor dengan sendirinya adalah definisi dari eksposur faktor portfolio, “eksposur” adalah pemahaman lain untuk melihat sejauh mana suatu portfolio terkait/berhubungan dengan perubahan (premia) yang terjadi di faktor-faktor tertentu.

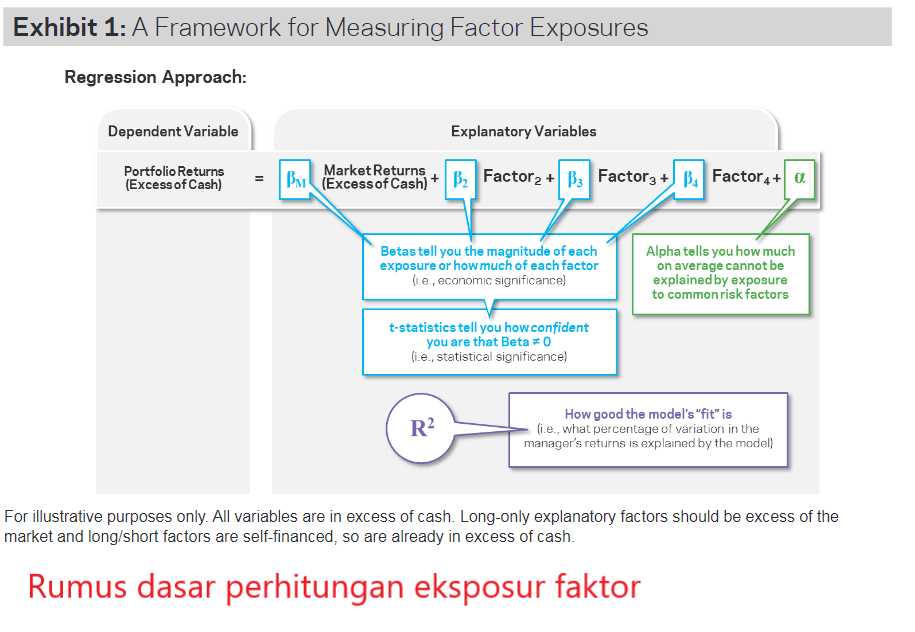
2. Rumus dasar perhitungan eksposur faktor

Berikut tertulis rumus-rumus perhitungan dasar bagi penilaian eksposur faktor suatu portfolio, beserta dengan penjelasannya (informasi pendekatan oleh hedge fund berfokus investasi faktor dengan nama “Applied Quantitative Research” (AQR)):

- Rumus untuk portfolio dengan satu faktor (single-factor portfolio), dengan contoh model faktor “Capital Asset Pricing Model” atau “CAPM”:

Pengembalian Portfolio (Di Atas Kas/Bebas Risiko) = (βm*Premia Faktor Pasar) + α

- Rumus untuk portfolio dengan banyak (lebih dari satu) faktor (multi-factor portfolio), dengan contoh model faktor “Fama-French 5 Factor Model” atau “FF5FM”:

Pengembalian Portfolio (Di Atas Kas/Bebas Risiko) = (βm*Premia Faktor Pasar) + (βsmb*Premia Faktor SMB) + (βhml*Premia Faktor HML) + (βrmw*Premia Faktor RMW) + (βcma*Premia Faktor CMA) + α

Penjelasan:
- “Pengembalian Portfolio (Di Atas Kas/Bebas Risiko)” adalah tingkat pengembalian yang seharusnya didapatkan oleh portfolio setelah dikurangi kas atau pengembalian aset bebas risiko lainnya
- “(βm*Premia Faktor Pasar)” adalah koefisien beta (factor loadings, “β”) bagi faktor pasar dari hasil regresi yang dikalikan dengan jumlah pengembalian premia faktor pasar sendirinya sesuai dengan definisi faktor yang tercantum
- “(βsmb*Premia Faktor SMB)” adalah koefisien beta (factor loadings, “β”) bagi faktor SMB (Small-Minus-Big) dari hasil regresi yang dikalikan dengan jumlah pengembalian premia faktor SMB sendirinya sesuai dengan definisi faktor yang tercantum
- “(βhml*Premia Faktor HML)” adalah koefisien beta (factor loadings, “β”) bagi faktor HML (High-Minus-Low) dari hasil regresi yang dikalikan dengan jumlah pengembalian premia faktor HML sendirinya sesuai dengan definisi faktor yang tercantum
- “(βrmw*Premia Faktor RMW)” adalah koefisien beta (factor loadings, “β”) bagi faktor RMW (Robust-Minus-Weak) dari hasil regresi yang dikalikan dengan jumlah pengembalian premia faktor RMW sendirinya sesuai dengan definisi faktor yang tercantum
- “(βcma*Premia Faktor CMA)” adalah koefisien beta (factor loadings, “β”) bagi faktor CMA (Conservative-Minus-Aggressive) dari hasil regresi yang dikalikan dengan jumlah pengembalian premia faktor CMA sendirinya sesuai dengan definisi faktor yang tercantum
- “α” adalah disebut sebagai “alpha” atau tingkat pengembalian portfolio yang tidak dapat dijelaskan oleh model faktor yang dipakai (output intercept positif), mempertunjukkan “performa di atas pasar” bagi portfolio sendirinya

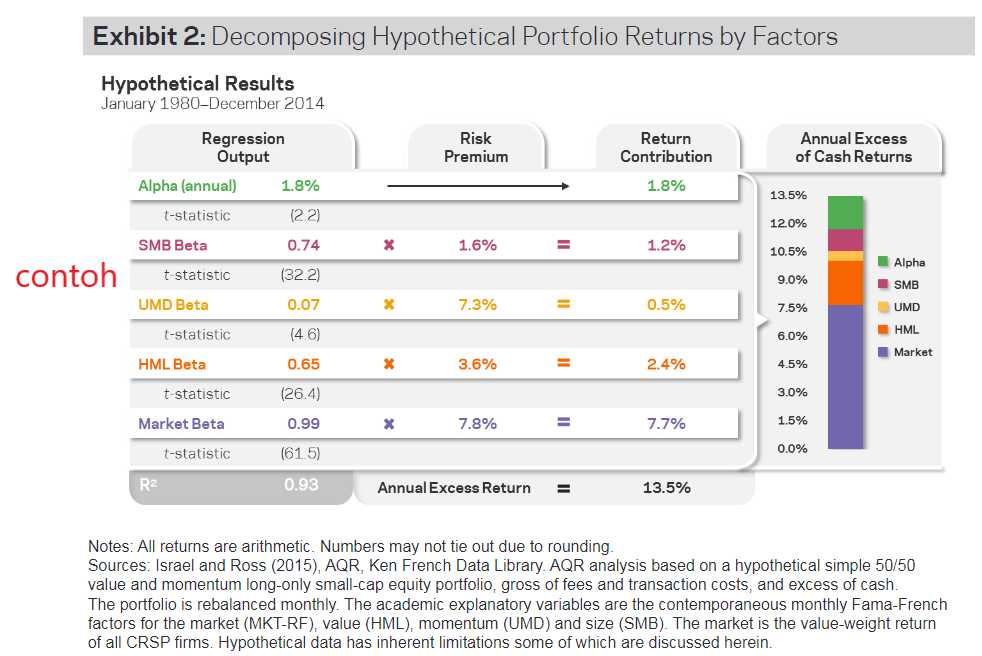
3. Pendefinisian dan konstruksi faktor

Pendefinisian dan konstruksi faktor berkaitan dengan bagaimana faktor dibentuk untuk mendapatkan premia, yang nantinya hendak dikalikan dengan koefisien beta agar mendapatkan premia ekspektasian bagi portfolio yang hendaknya menargetkan/memiliki eksposur terhadap faktor tersebut. Faktor pada umumnya bersifat akan memiliki 2 “kaki” atau “legs”, yakni “long-leg” dan “short-leg” - subtraksi oleh long-leg relatif terhadap short-leg merupakan cara yang umum untuk menentukan premia dari suatu faktor. Berikut sekumpulan contoh definisi dan konstruksi akan faktor-faktor dari FF5FM (penting: semua “kelebihan” atau “excess returns” adalah positif):

- Faktor Pasar (Rm-Rf) : Didefinisikan sebagai kelebihan (excess returns) dari pengembalian pasar saham yang telah dikurangi pengembalian aset bebas risiko, umum dikuantifikasi/dikonstruksi sebagai “market-cap weight returns - risk-free returns”
- Faktor Ukuran (SMB): Didefinisikan sebagai rata-rata kelebihan (excess returns) dari pengembalian kelompok saham kecil yang telah dikurangi pengembalian kelompok saham besar - mengingat netralitas dari faktor lainnya, umum dikuantifikasi/dikonstruksi sebagai “1/3 (SMB(b/m) + SMB(op) + SMB(inv))”
- Faktor Nilai (HML): Didefinisikan sebagai rata-rata kelebihan (excess returns) dari pengembalian kelompok saham dengan P/BV rendah yang telah dikurangi pengembalian kelompok saham dengan P/BV tinggi - mengingat netralitas ukuran, umum dikuantifikasi/dikonstruksi sebagai “1/2 (Small Value + Big Value) - 1/2 (Small Growth + Big Growth)”
- Faktor Profitabilitas (RMW): Didefinisikan sebagai rata-rata kelebihan (excess returns) dari pengembalian kelompok saham dengan GP/A tinggi yang telah dikurangi pengembalian kelompok saham dengan GP/A rendah - mengingat netralitas ukuran, umum dikuantifikasi/dikonstruksi sebagai “1/2 (Small Robust + Big Robust) - 1/2 (Small Weak + Big Weak)”
- Faktor Investasi (CMA): Didefinisikan sebagai rata-rata kelebihan (excess returns) dari pengembalian kelompok saham dengan tingkat investasi rendah yang telah dikurangi pengembalian kelompok saham dengan tingkat investasi tinggi - mengingat netralitas ukuran, umum dikuantifikasi/dikonstruksi sebagai “1/2 (Small Conservative + Big Conservative) - 1/2 (Small Aggressive + Big Aggressive)”

Dapat dilihat bagaimana seluruh faktor memiliki “long-leg” dan “short-leg” (terkecuali faktor pasar, yang dengan sendirinya hanya merupakan kelebihan pengembalian pasar saham relatif terhadap pengembalian aset bebas risiko). Dari faktor ukuran yang merupakan perbedaan pengembalian di antara saham kecil (long-leg) vs. saham besar (short-leg), perbedaan pengembalian saham dengan P/BV rendah (long-leg) vs. saham dengan P/BV tinggi (short-leg) untuk faktor nilai, perbedaan pengembalian di antara saham GP/A tinggi (long-leg) vs. saham dengan GP/A rendah (short-leg) untuk faktor profitabilitas, hingga perbedaan pengembalian saham dengan tingkat investasi rendah (long-leg) vs. saham dengan tingkat investasi tinggi (short-leg) untuk faktor investasi. Disimpulkan, premia faktor secara umum didefinisikan sebagai pengembalian lebih (positif) dari hasil subtraksi pengembalian kelompok saham long-leg yang telah dikurangi pengembalian kelompok saham short-leg (premia faktor = long leg - short leg).

4. Regresi linear sebagai instrumen pengukur eksposur faktor

Regresi linear merupakan suatu pendekatan statistik untuk mengetahui hubungan dan pengaruh yang dimiliki oleh satu/lebih variabel terhadap variabel lainnya. Pada dasarnya, regresi linear memiliki 2 fungsi utama: 1. Mengetahui jika variabel penjelas memiliki kemampuan untuk memprediksi outcome dari variabel respons (dependen) dengan baik, dan 2. Mengetahui seberapa besar sensitivitas pengaruh yang dimiliki oleh variabel-variabel penjelas terhadap variabel respons. Regresi linear berupaya untuk membentuk hubungan kuantitatif (empiris) di antara 2 variabel dependen (respons) dan independen (penjelas). Model regresi linear sendirinya umum datang dalam 2 bentuk yang mencakupi “regresi linear sederhana” (simple linear regression) yang meliputi 1 variabel dependen dan 1 variabel independen, serta dengan bentuk “regresi linear berganda” (multiple linear regression) yang meliputi 1 variabel dependen dan lebih dari 1 variabel independen (terdapat jenis regresi lainnya seperti; logistic regression, ordinal regression, multinomial regression, dan discriminant analysis - hanya jenis-jenis regresi lain tersebut tidak (terlalu) umum dipakai di analisis faktor seperti keseringan pemakaian model regresi linear sederhana dan berganda).

Di dalam konteks sejarah singkat, regresi pada awalnya diaplikasikan oleh Sir Francis Galton di tahun 1885 (abad ke-19) untuk menemukan konsep “regression to the mean” pada perbedaan tinggi badan anak-ayah. Ia menemukan bahwa, secara rata-rata, anak laki dengan ayah tinggi cenderung akan menjadi lebih tinggi dari pada anak laki dengan ayah rendah, tetapi terdapat perbedaan di antara tinggi anak tinggi/rendah dengan ayah tinggi/rendahnya tersendiri, anak tinggi/rendah cenderung menjadi lebih sedikit rendah/tinggi dari pada ayahnya, yang mengakibatkan, dalam kelamaan, tinggi anak laki yang cenderung dinormalisasi pada rata-rata (mean) untuk waktu berkepanjangan. Penemuan Galton merupakan pemicu utama akan metode regresi yang hendaknya dipakai secara umum pada berbagai bidang ilmu kontemporer sekarang, termasuk tetapi tidak terbatas pada analisis empiris di pasar modal.

Bagi analisis eksposur faktor sendirinya, diperlukan 2 komponen data - yakni: 1. Data historis time-series variabel dependen, dan 2. Data historis time-series variabel independen. “Time-series” dapat dipahami sebagai sekuensi data di dalam satu jangkau periode waktu, sebagai contoh: variabel “a” memiliki sekuensi data di periode 2010-2020 (tahunan), maka data tersebut hendaknya dipaparkan pertahun dari (termasuk) tahun 2010 hingga (termasuk) tahun 2020 = -13.45 (2010 awal), -9.16, 30.19, 37.66, -11.63, -22.13, -34.74, -0.52, 45.8, 42.86, 21.69 (2020 akhir) (sekuensi data merupakan contoh dari data historis time-series). Kemudian data historis time-series variabel dependen hendaknya diregresikan terhadap data historis time-series variabel independen yang pada akhirnya akan menyelesaikan proses regresi linear tersendiri - ini berfungsi untuk mendapatkan “koefisien beta” (“β”) (lihat bagian 2 sebelumnya, “rumus dasar perhitungan eksposur faktor”) sebagai penilai sensitivitas portfolio terhadap premia faktor yang ditargetkan (setelah koefisien beta dikalikan dengan premia faktor). Proses regresi linear dapat dilakukan secara manual melalui hitungan kalkulator, tetapi, pendekatan lebih umum (dan modern) sekarang adalah dengan memakai aplikasi atau alat untuk mengotomatisasikan proses regresi - alat umum seperti regresi linear di R, Excel, hingga aplikasi pihak ketiga lainnya umum dipakai untuk mempercepat (dan mensimplifikasi) proses regresi.

5. Sekumpulan asumsi di belakang regresi linear

Di dalam regresi linear terdapat beberapa asumsi yang hendaknya dipenuhi agar hasil output dari model regresi memiliki reliabilitas yang tinggi, pelanggaran akan asumsi hendaknya dapat menyebabkan error (kesalahan) output dari hasil regresi sendirinya. Secara umum (dan singkat), terdapat 5 asumsi di balik model regresi linear:

- Asumsi hubungan linear: asumsi ini mempertunjukkan bahwa hendaknya terdapat hubungan linear (lurus) di antara variabel dependen dan independen, input bagi model hendaknya juga memerhatikan nilai ekstrem yang dapat berpengaruh signifikan akan output
- Asumsi normalitas: asumsi ini menekankan bagi model regresi linear untuk memiliki (input) plot data yang di distribusikan mengikuti distribusi normal (gaussian distribution) dengan tidak terdapatnya distribusi non-normal (skewness, dan lainnya)
- Asumsi tiada (atau minim) multikolinearitas: asumsi bahwa variabel-variabel independen hendaknya tidak memiliki korelasi yang tinggi dengan satu sama lain
- Asumsi tiada (atau minim) autokorelasi: asumsi bahwa residual (perbedaan nilai observasi dan nilai prediksi) hendaknya independen dari satu sama lain
- Asumsi homoskedastisitas: asumsi bahwa plot residual berada di dekat garis regresi

6. Interpretasi output penting dari hasil regresi linear

Regresi linear sendirinya memiliki banyak output yang hendak diperhatikan, tetapi secara umum, 3 output utama hendaknya telah memberi tahu informasi yang cukup lengkap untuk mengetahui hubungan di antara variabel-variabel yang di uji coba, 3 output tersebut mencakupi:

- R^2 (r-squared): r-squared atau yang disebut juga sebagai “koefisien determinasi” adalah output model regresi linear yang berfungsi untuk memberi penilaian akan seberapa baik model (yang terdiri dari variabel-variabel independen) dalam menjelaskan/memprediksi variasi dari variabel dependen. Sebagai aturan, semakin tinggi nilai R^2 maka semakin baik pula model dan variabel independen dalam menjelaskan variasi variabel dependen sendirinya. Nilai R^2 umum terletak di antara 0% (0) hingga 100% (1) (tetapi terkadang nilai R^2 dapat negatif jika model regresi sangat buruk). Nilai R^2 penting bagi model regresi untuk memastikan model regresi yang dipakai adalah model yang baik (“fit”). Nilai R^2 50% (0.5) bagi ilmu sosial dapat dikatakan sebagai nilai yang cukup baik (walaupun tidak sempurna), nilai R^2 rendah menunjukkan bahwa model regresi tidak merupakan “fit” yang baik (variabel independen tidak memiliki pengaruh terhadap variabel dependen)
- t-stat (t-statistic): T-stat atau t-statistic adalah suatu pendekatan uji hipotesis untuk menentukan jika variabel independen adalah prediktor signifikan untuk variabel dependen, prediktor signifikan yang bukan hanya sekedar keberuntungan. T-stat umumnya signifikan di angka 2 ke atas (95% confidence interval), tetapi nilai dapat berbeda tergantung data. T-stat di bawah nilai yang signifikan menunjukkan bahwa pengaruh koefisien beta variabel independen terhadap variabel dependen tidak berbeda jauh dari sekedar keberuntungan
- “β” (koefisien beta/beta coefficient): “β” atau koefisien beta adalah tingkat sensitivitas yang dimiliki oleh variabel independen dalam memengaruhi prediksi variabel dependen, nilai “β” dapat berbentuk positif maupun negatif, semakin jauh dari 0 (baik negatif maupun positif) maka sensitivitas pengaruh variabel independen ke variabel dependen semakin tinggi (catatan: koefisien beta, di dalam konteks analisis eksposur faktor, sering juga disebut sebagai “factor loadings”)

Saran: hendaknya baik untuk membaca hasil regresi linear dari R^2 terlebih dahulu kemudian membaca t-stat, dan akhirnya β, untuk memberi perhatian jika model merupakan fit yang baik dan jika beta signifikan terlebih dahulu.

7. Sekumpulan kesalahan dalam menilai eksposur faktor portfolio

Berikut tertulis beberapa kesalahan dalam melakukan penilaian akan eksposur faktor, (sebagian) berdasarkan komentar dari AQR (terutama di dalam konteks penilaian eksposur faktor portfolio):

- Tidak cukup fokus ke nilai R^2, tidak memerhatikan jika model merupakan fit yang baik atau tidak
- Terlalu banyak fokus ke koefisien beta (β) dan tidak cukup fokus ke t-stat, β variabel independen dapat memiliki nilai tinggi, tetapi jika t-stat tidak signifikan maka nilai tinggi β sendirinya adalah hanya sekedar keberuntungan
- Tidak memerhatikan biaya transaksi yang dapat memengaruhi output model
- Analisis akan perusahaan yang sangat kecil dan ilikuid, menghasilkan hasil regresi tidak praktis walaupun model merupakan fit yang baik
- Tidak memerhatikan bagaimana faktor didefinisikan atau dikonstruksikan, faktor nilai (value factor, “HML”) dapat memberikan data time-series yang berbeda jika didefinisikan sebagai P/BV dan bukan P/E (pemakaian definisi dan konstruksi berbeda dapat memengaruhi input data model regresi)
- Terdapat pengaruh implisit dari faktor lainnya (pengaruh sektor, risiko sekuritas individu, dll)

8. Penentuan “alpha” melalui output “intercept”

Ketika melakukan penilaian terhadap performa manajer investasi dalam mengelola reksadana dengan pendekatan manajemen aktif (stock picking, bukan indexing terhadap indeks representatif pasar), hendaknya dilakukan penilaian jika manajer tersebut telah melengkapi janji “outperformance” (performa melebihi) relatif terhadap indeks acuan (benchmark index) (yang dengan sendirinya adalah tujuan utama manajemen aktif portfolio), salah satu cara penilaian terhadap performa manajer investasi aktif tersebut adalah dengan melakukan regresi linear data time-series historis performa reksadana yang dibandingkan dengan faktor-faktor prediktor pengembalian seperti faktor pasar, SMB, HML, RMW, CMA, dan lainnya.

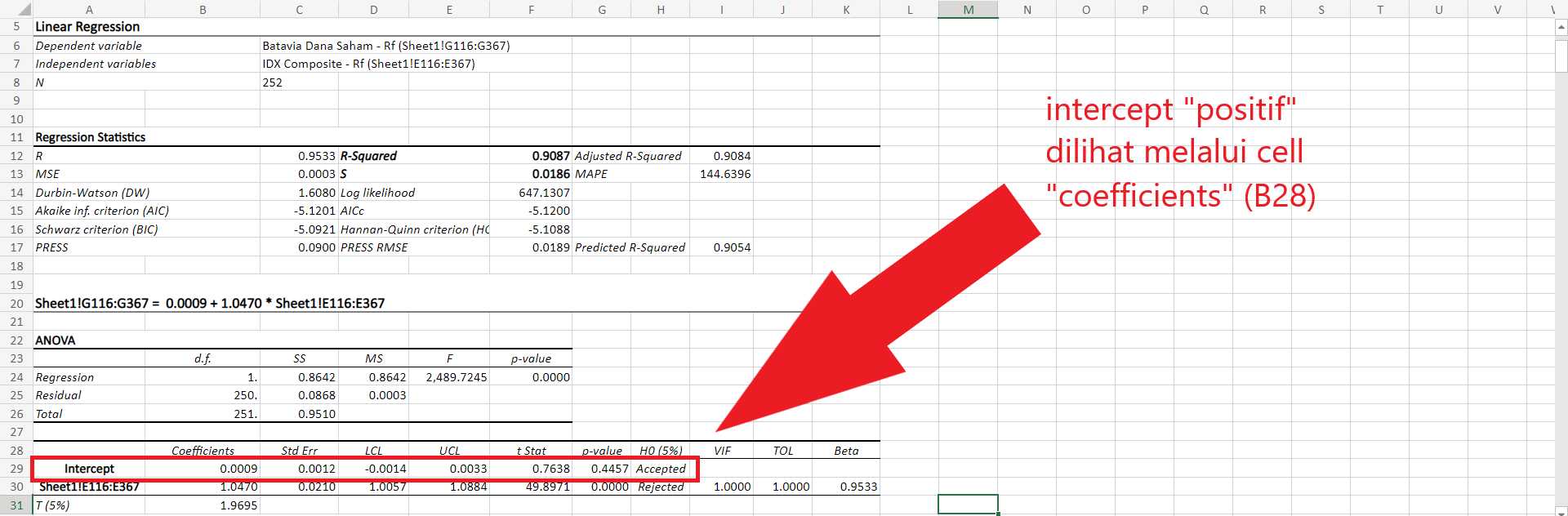
“intercept” (atau “constant”) dari hasil output regresi berfungsi untuk memenuhi tujuan (penilaian performa) tersebut dengan intercept sendirinya yang menunjukkan (di dalam konteks analisis performa manajer investasi aktif) tingkat pengembalian yang tidak dapat dijelaskan oleh faktor-faktor independen/prediktor (alpha). Sebagai aturan: 1. Nilai intercept positif dan t-stat signifikan menunjukkan MI aktif yang mengalahkan kinerja pasar (alpha), 2. Nilai intercept positif dan t-stat tidak signifikan menunjukkan MI aktif yang “beruntung” untuk mengalahkan kinerja pasar (alpha, keberuntungan), 3. Nilai intercept negatif dan t-stat signifikan menunjukkan MI aktif yang underperform/gagal mengalahkan kinerja pasar, dan 4. Nilai intercept negatif dan t-stat tidak signifikan menunjukkan MI aktif yang “beruntung” (tidak definitif) underperform/gagal mengalahkan kinerja pasar. Penilaian MI aktif dengan memakai regresi linear multi-faktor dapat memberi gambaran yang lebih lengkap jika MI tersebut benar-benar mengalahkan pasar dengan membawa informasi baru kepada harga saham atau jika MI tersebut hanya memiliki “eksposur” terhadap faktor-faktor yang dapat memberi pengembalian melebihi pasar - jika MI hanya menargetkan faktor-faktor seperti nilai, momentum, dan lainnya, maka MI tersebut sebenarnya tidak memberi value-add kepada client-investor dan hanya mengambil fee besar melalui expense ratio tinggi dari uang calon investor yang diinvestasikan dengan MI aktif tersebut (karena umum terdapat “reksadana faktor” pasif sebagai alternatif yang dapat memberi performa eksposur faktor dengan expense ratio yang jauh lebih murah).

[GAMBAR 1, intercept]

9. Contoh nyata penilaian eksposur faktor portfolio

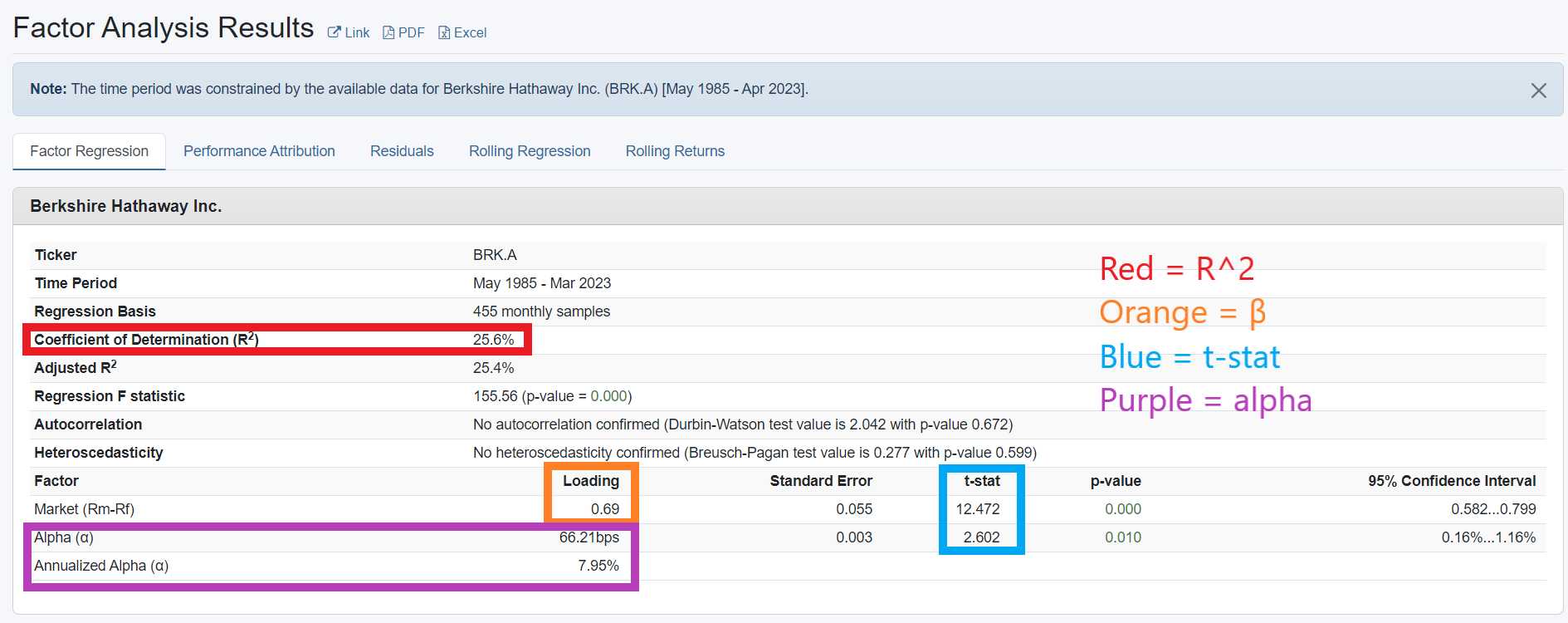
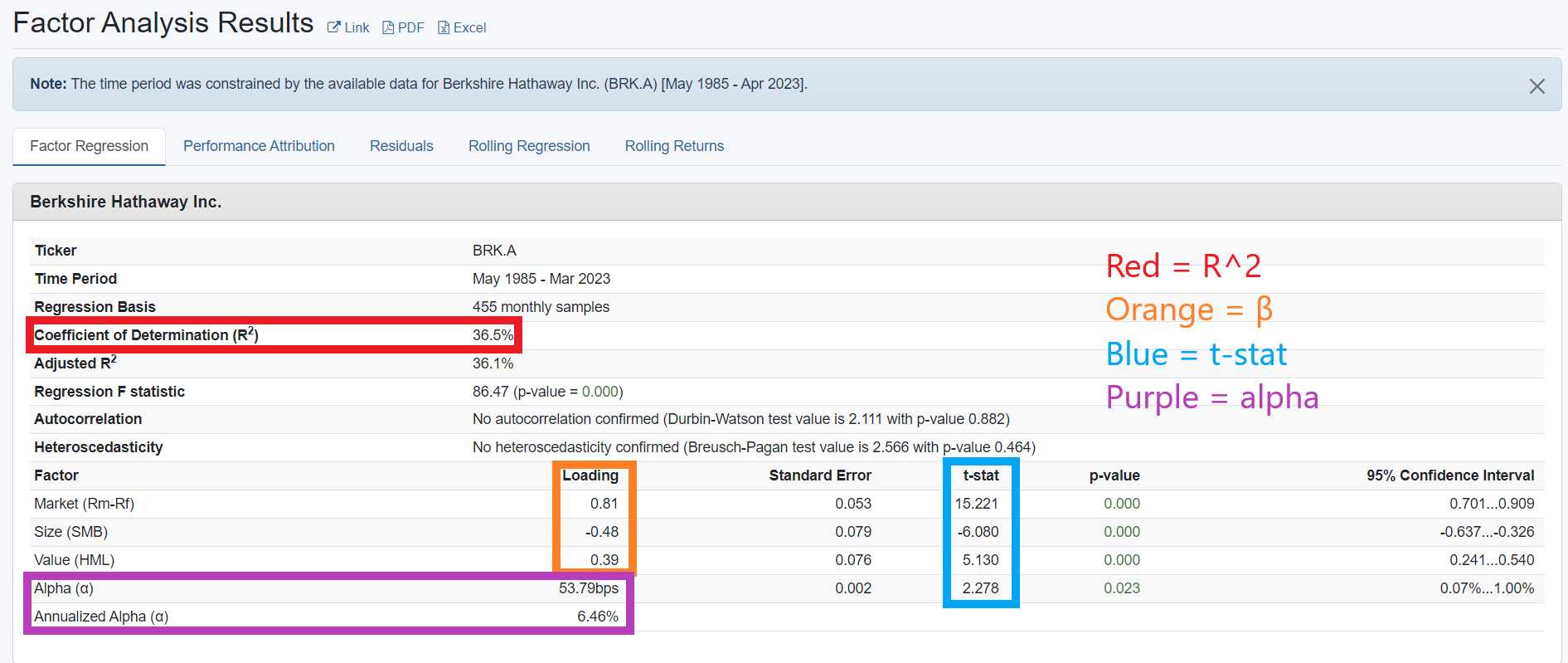
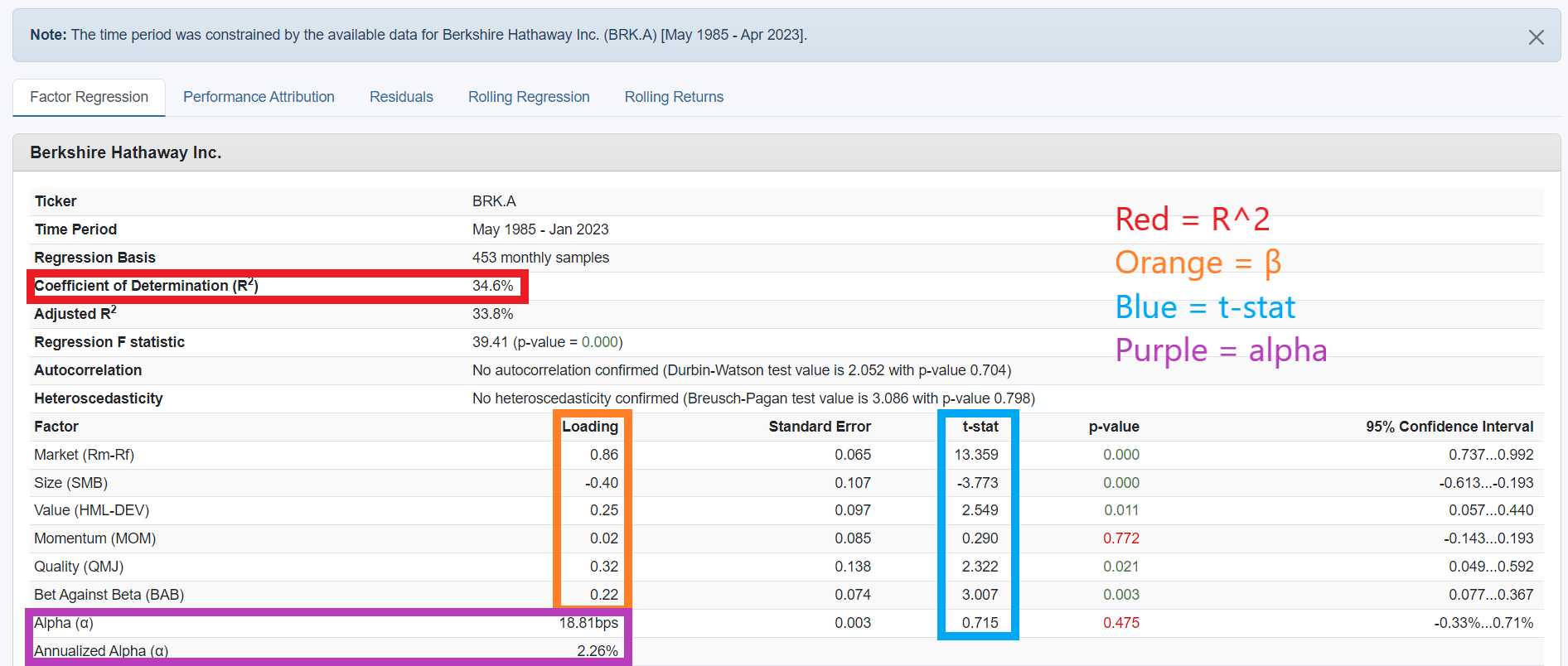
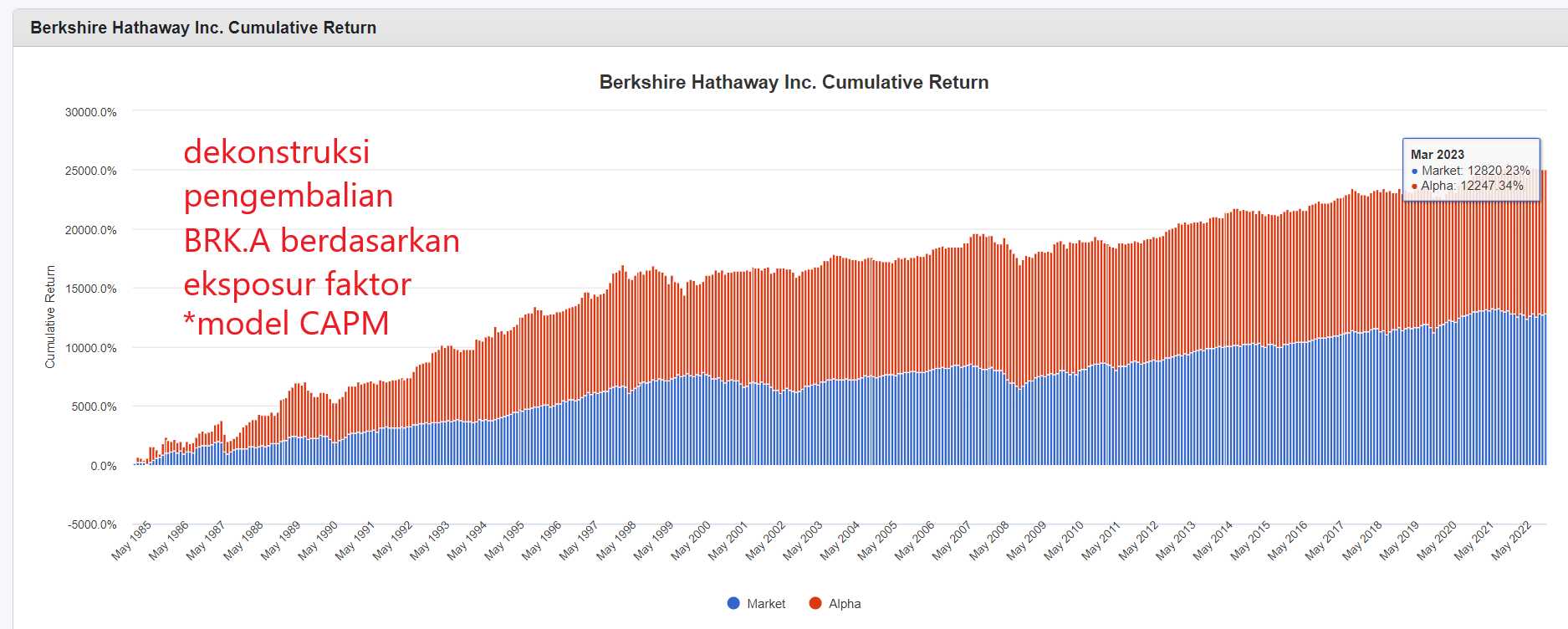
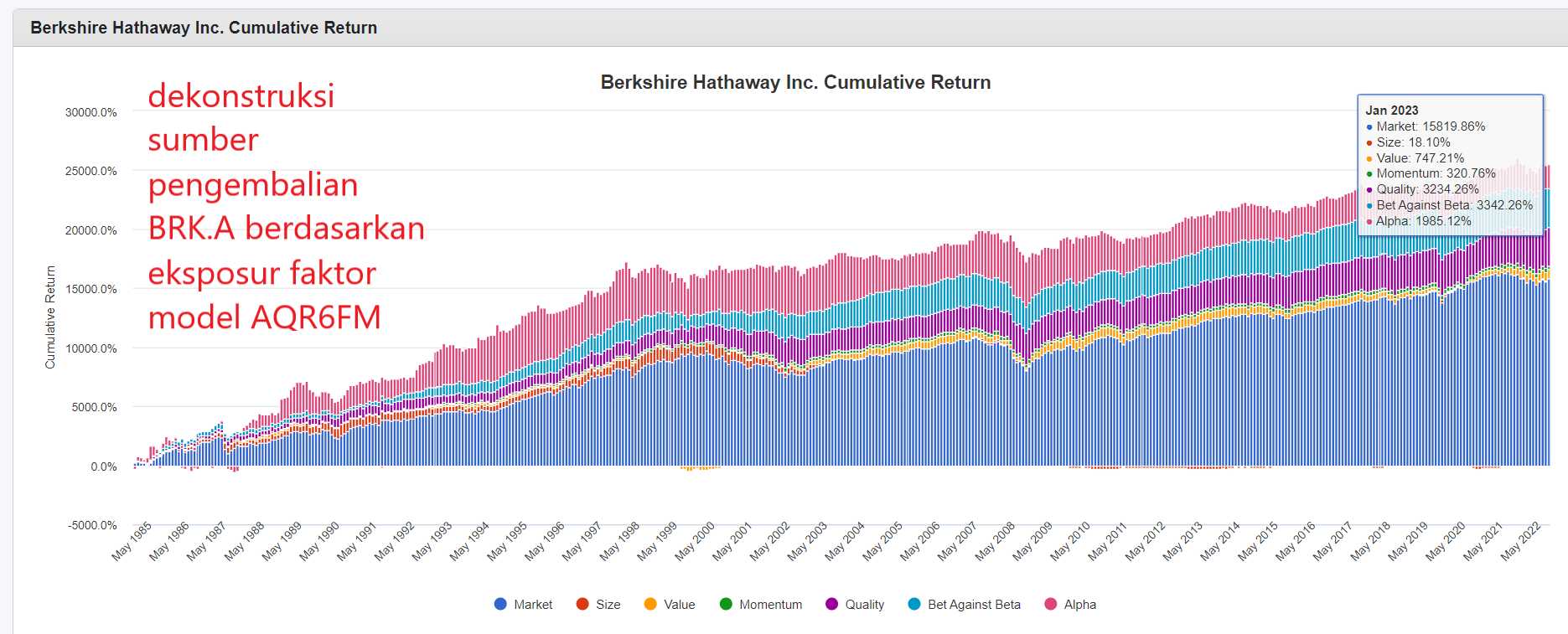
Di contoh berikut saya hendak mepertunjukkan regresi linear dengan model 1 faktor CAPM Fama-French (gambar 2), model 3 faktor pasar, SMB, HML Fama-French (gambar 3), dan model 6 faktor pasar, SMB, HML-DEV, MOM, QMJ, BAB AQR (gambar 4) terhadap saham BRK.A (Berkshire Hathaway Class A Shares) (detail: metode regresi adalah OLS dengan rolling regression period 12 bulan, periode time-series 1985-2023, data Amerika Serikat, basis regresi bulanan).

[GAMBAR 2, BRK.A CAPM]

[GAMBAR 3, BRK.A FF3FM]

[GAMBAR 4, BRK.A AQR6FM]

Hasil regresi mempertunjukkan bahwa BRK.A terhadap ketiga model regresi faktor memiliki R^2 yang rendah di 25% hingga 35%. Gambar 2 menunjukkan BRK.A memiliki eksposur faktor dengan t-stat signifikan di faktor “Market” dengan β 0.69 - alpha positif 66.21 bps dengan t-stat signifikan, gambar 3 menunjukkan BRK.A memiliki eksposur faktor dengan t-stat signifikan di faktor “Market” “Size” dan “Value” dengan respektif β 0.81 -0.48 dan 0.39 untuk setiap faktor - alpha positif (tetapi berkurang) di 53.79 bps dengan t-stat signifikan, gambar 4 menunjukkan BRK.A memiliki eksposur faktor dengan t-stat signifikan di faktor “Market” “Size” “Value” “Quality” “Bet Against Beta” dengan respektif β 0.86 -0.40 0.25 0.32 0.22 serta dengan eksposur tidak signifikan (t-stat rendah) di faktor “Momentum” dengan β 0.02 - alpha tetap positif tetapi tidak lagi signifikan dengan nilai 18.81 bps.

Menurut sudut pandang model CAPM, BRK.A menghasilkan alpha, tetapi setelah mengendalikan untuk faktor-faktor selain faktor pasar, BRK.A ditemukan untuk menargetkan saham-saham dengan ciri-ciri ukuran besar, valuasi murah, kualitas tinggi, dan volatilitas rendah - setelah mengetahui eksposur faktor BRK.A, alpha yang dimiliki oleh saham menghilang (menjadi tidak signifikan). Inilah yang dimaksud dengan “alpha” ketika penilaian performa MI aktif dilakukan, menyesuaikan pengembalian portfolio MI aktif dengan faktor-faktor penjelas, jika pengembalian masih signifikan walaupun telah mengendalikan untuk eksposur faktor-faktor lainnya, maka MI aktif tersebut menghasilkan “alpha” (mengalahkan pasar).

10. Peringatan singkat tentang regresi linear

Hendaknya disebutkan secara singkat/sedikit peringatan terkait regresi linear. Karena regresi linear sendiri bagi penilaian eksposur faktor portfolio berupaya untuk mencari sumber pengembalian independen dari portfolio sendirinya, maka peneliti studi ekonomi keuangan cenderung melakukan hal yang disebut dengan “data mining”. Data mining dapat dipahami sebagai upaya pencarian korelasi di antara 2 variabel walaupun tidak terdapat hubungan jelas di antara 2 variabel tersebut (korelasi palsu), literatur studi ekonomi keuangan tentang faktor berisi penuh dengan hasil data mining, “faktor” hasil data mining tidak diekspektasi untuk memberi premia positif out of sample/di masa depan, maka layaknya “faktor” hasil data mining tersebut dihindari - dan tetap waspada akan korelasi palsu yang tidak didukung oleh teori ekonomi di baliknya ketika melakukan praktik regresi.

11. Poin kesimpulan

- Eksposur faktor berfungsi untuk menilai sensitivitas portfolio terhadap premia faktor yang ditargetkan, hanya karena portfolio menargetkan faktor belum tentu portfolio tersebut dapat secara penuh merealisasi premia faktor secara menyeluruh
- β*premia faktor = eksposur faktor (kontribusi pengembalian)
- Untuk mendapatkan nilai “premia faktor” perlu memerhatikan definisi dan konstruksi dari faktor sendirinya, dengan premia faktor = long leg - short leg
- Untuk mendapatkan “β” (beta) perlu dijalankan regresi linear bagi portfolio dengan faktor-faktor yang ditargetkan melalui data historis time-series
- Lengkapi asumsi di belakang model regresi linear untuk hasil yang baik
- Fokus kepada hasil output R^2, t-stat, β, dan alpha

12. Catatan lainnya

Tulisan ini hanya pengenalan akan pendekatan regresi dan metode ekonometrik yang umum dipakai di studi penilaian aset, jika terdapat kesalahan mohon tulis di komentar dan referensikan sumber perbaikan. Matematika di tulisan juga saya simplifikasi dan batasi agar lebih mudah dicerna.

Referensi:
- Back to Basics: What is Econometrics?, IMF, https://cutt.ly/Mwqk7uk1
- Measuring Portfolio Factor Exposures: A Practical Guide, AQR, https://cutt.ly/Cwqk7uDG
- Description of Fama/French 5 Factors (2x3), Ken. French. Library, https://cutt.ly/Wwqk7uBi
- What is Linear Regression?, Statistics Solutions, https://cutt.ly/Jwqk7u5F
- Introduction to Linear Regression, Duke, https://cutt.ly/iwqk7izB
- Assumptions of Linear Regression, Statistics Solutions, https://cutt.ly/9wqk7iWl

Sumber daya: https://cutt.ly/zwqk7i20

tags: $IHSG $BBCA $TLKM $ASII $UNVR